Material Properties
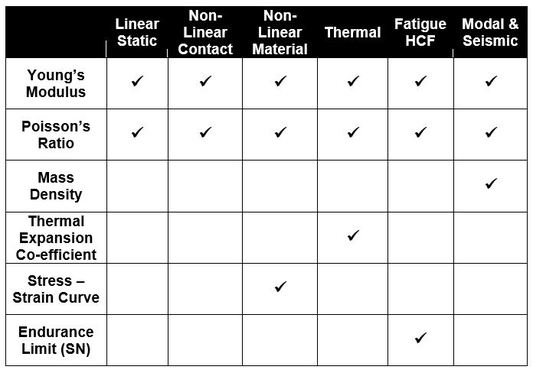
The following table shows the minimum material properties that are required for common types of analysis. Various material databases can be found online or data can be obtained from material testing.
Young's Modulus
Young’s modulus is basically the stiffness of a material. For a stiff material such as steel at room temperature it is typically 205 GPa or 205,000 MPa. For a soft material such as nylon it may be 3 GPa or 3000 MPa.
Most material data is published at room temperature so if your parts have a high or low operating temperature you need to ensure you are using the correct value of Young’s Modulus.
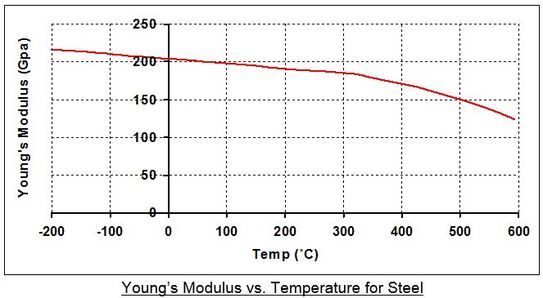
The following graph shows Young's Modulus versus temperature for steel.
Most material data is published at room temperature so if your parts have a high or low operating temperature you need to ensure you are using the correct value of Young’s Modulus.
The following graph shows Young's Modulus versus temperature for steel.
From observing the above a graph it can be seen that a steel component will deform much more at elevated temperatures. This in turn will affect its natural frequency.
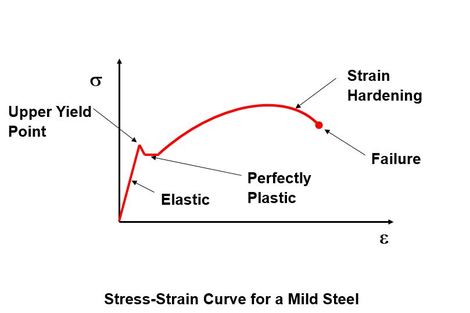
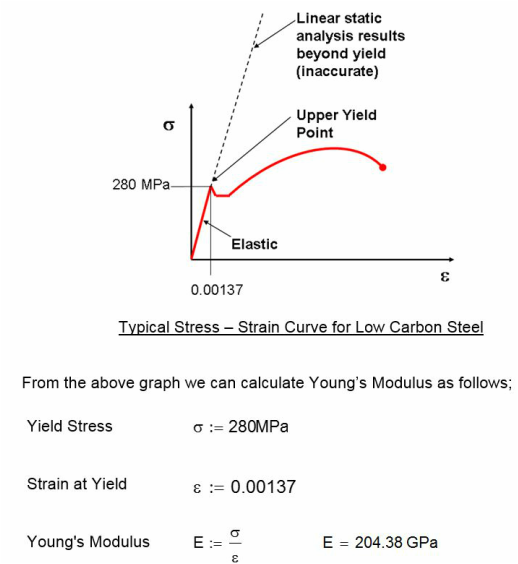
Young’s Modulus is basically the slope of the straight elastic part of the stress-strain curve as shown in the graph below.
Young’s Modulus is basically the slope of the straight elastic part of the stress-strain curve as shown in the graph below.
Linear static analysis applied to the majority of FEA models follows the principle of Hooke’s Law of elasticity. i.e. the stiffness of the part follows the elastic portion of the stress strain curve.
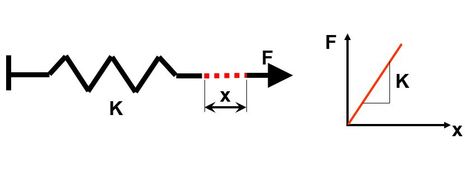
Think of the linear static FEA model as a spring.
Think of the linear static FEA model as a spring.
Hooke’s Law has a linear relationship between force and displacement where K is the force constant, F is the restoring force and x is the displacement.
F = K.x
Components that regain their original shape after a load has been applied are usually operating in the elastic region of the stress – strain curve and obey the principles of Hooke’s Law.
The relationship of stress, strain and Young’s Modulus is as follows;
F = K.x
Components that regain their original shape after a load has been applied are usually operating in the elastic region of the stress – strain curve and obey the principles of Hooke’s Law.
The relationship of stress, strain and Young’s Modulus is as follows;
Tip
Young’s Modulus only affects displacement and not stress on a single part. On an assembly with multiple parts of different values of Young’s Modulus, it could also change force transfer distribution and hence stress.
Young’s Modulus (E) can be calculated from the stress strain curve. Low carbon steel has a typical stress - strain curve that is elastic until yield before becoming plastic.
Tip
For ductile materials such as steel any stress or deflection from FEA that is higher than the yield point of the material is not accurate. If you need to know how much your component will permanently deform beyond yield you need to perform non-linear material analysis.
For linear static analysis if you double the load you will also double the displacement up to yield. This does not apply to some materials for example; some plastics do not obey Hooke’s law.
For ductile materials such as steel any stress or deflection from FEA that is higher than the yield point of the material is not accurate. If you need to know how much your component will permanently deform beyond yield you need to perform non-linear material analysis.
For linear static analysis if you double the load you will also double the displacement up to yield. This does not apply to some materials for example; some plastics do not obey Hooke’s law.
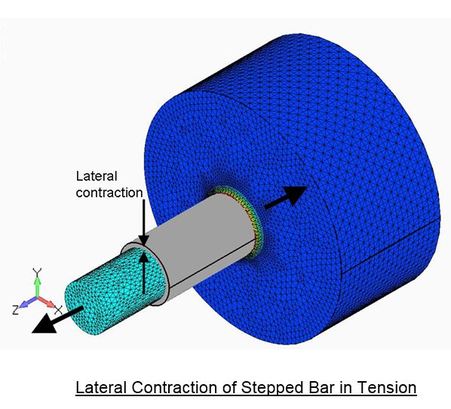
The Effects of Poisson's Ratio
Poisson's ratio is a measure of the lateral contraction of a material when under tensile stress in the longitudinal direction. For most cases it has little effect on the results but for a few it is significant. Poisson’s ratio varies from 0.2 for some grades of cast iron to 0.45 for some grades of polythene.
Tip
For linear static analysis on a single part you only need Young’s Modulus and Poisson’s Ratio for your FEA model and the other material properties can be left blank.
For linear static analysis on a single part you only need Young’s Modulus and Poisson’s Ratio for your FEA model and the other material properties can be left blank.